在網路上有一篇文章 The Physics Of Snowboarding ,談到雪地滑板的物理學,把一般滑行,割雪滑行,甚至到半管滑行,就物理學的角度來探討雪地滑板。原文很長,非物理相關科系看起來有點吃力,所以我們請到了滑板基地的夥伴-趙元,同時也是名出色的物理博士來味大家解說雪地滑板滑行物理學。(同文也在趙元博士的布洛格中)
[toc]
雪地滑板滑行物理學
了解雪板滑雪背後的物理,將有助於提升技術層次,了解關鍵原理可以幫助做出正確的動作,更可以改善滑雪表現。
滑雪是一個將「重力位能」轉換成前進速度的「動能」的一項運動。所以當往山谷下滑愈多,就會有更快的速度。第一張圖是說明在陡坡上,可以靠著Z字形的方式來有效控制速度。而玩 heliski / helisnowboard 可以從直昇機上一躍而下而不受傷,則是因為山坡是一個斜面,真正正面衝擊的分量只佔一小部份。
圖中可以看出其實該雪友是帶邊在滑的,可以藉由板子與雪的摩擦力來降低滑行的速度。不過相對於使用carving轉彎,skidding是比較不好的方式。
(這次去 La Thuile 會議的主辦單位有安排ski教練。基本上ski與SB一樣,高級轉彎應該用carving的方式,能夠在不降低速度的方式轉彎。像我這種不管ski還是SB都帶邊在滑的,就被訓了說,不學好carving技術是會停頓無法提升的… 泣)

首先是帶邊的犛式轉彎 (Skidding)
這是初中級或是比較沒有經驗的SB雪友的轉彎方式:雪板以斜面「掃過」雪面,甚至是正面在「鏟雪」。因此最後在滑行的速度上,會有相當程度的損失。這是因為這裡板與雪的摩擦力,遠遠大於打直板平面滑行時的狀態。
以carving的方式,你可以保持前進的運動方向,與雪板方向平行。在這裡板與雪的摩擦力很小, 就可以以更快的速度通過雪道。(是進階板友的高級轉彎方式)
割雪轉彎 (Carving)
雪板的側邊(side cut)是做成一個弧度的,這個弧度的曲率半徑Rsc,就是理想上轉彎的迴轉半徑Rt。(pure carving)
但是當雪板面與雪面有一個交角Phi的時候,這個板邊弧度投影在雪面上,就會受到影響,實際的有效曲率半徑就變成了 Rsc Cos(phi),這時雪板就走在一個橢圓邊上。這樣子一來,無可避免的,就會增加轉彎時 skidding 的量,進而增加摩擦力影響到滑行的速度。當板子做成反曲(?)的形狀(reverse camber),雪板邊就能夠即使在不與雪面平行時,仍然走在Rt’ = cos(phi)的正圓邊上。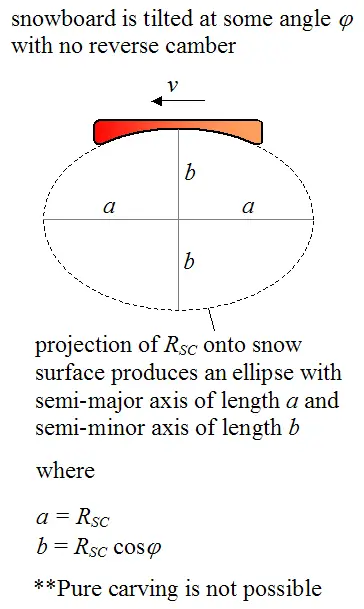
深入割雪轉彎
基本上,最大的 reverse camber 取決於板與雪面的角度 phi,還有板子的側邊曲率半徑。一個側邊曲率半徑比較小的板子,就可以接受更大的 reverse camber,來轉一個更小半徑的彎。有經驗的選手可以根據實際的地形,來調整板子與雪面的角度,來達成不同的迴轉半徑。
如何在割雪轉彎 (carving turn) 下保持平衡
先前提到的,理想的轉彎是以完全割雪轉彎的方式來完成,這樣子可以把因轉彎而損失的速度降到最低。以下來分析割雪轉彎中各種力的平衡。
首先是定義座標與代號,由重力方向造成的效果隨滑雪者的行進方向改變。
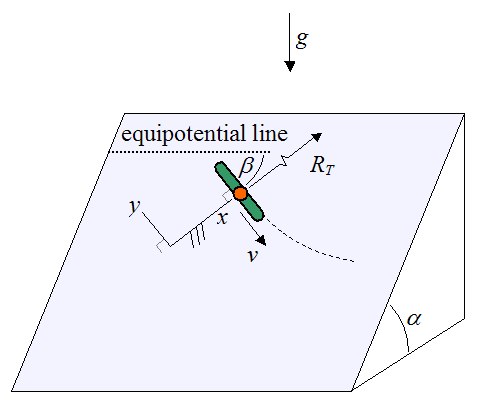
- g 重力加速度,地球上是 9.8 m/s^2
- alpha 是坡度,零度代表水平面
- beta 是雪板行進方向與水平線的交角,水平線與重力方向垂直
- R_T 是轉彎的旋轉半徑
- v 是滑雪者切線方向的速度,指向滑雪者的行進方向。
這裡我們定義 x-y 平面,讓 y 軸垂直於坡面,而 x 軸在坡面上與行進方向垂直。
(為了簡化起見,這裡我們假設坡面是一個平面,忽略三維的效應) 再來我們看相對於滑雪者的座標規劃。
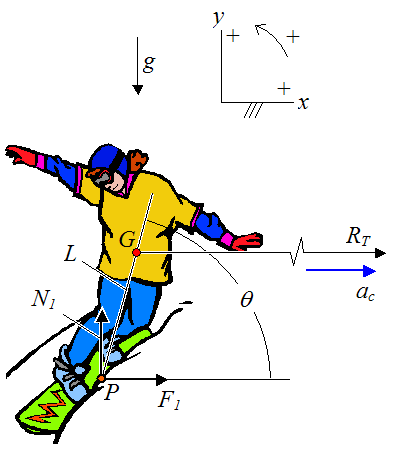
- theta 是坡面上的 x 軸與滑雪者身體重心的交角,也就是滑雪者傾斜與雪面的交角。
- G 是滑雪者的質量中心,這包含了滑雪者與雪板,整個視為一個剛體。
- P 是雪板與雪面接觸的近似點。
- L 是重心 G 與 P 點的距離
- a_c 是位於 G 點的向心加速度,方向指向 x 軸向迴轉半徑的圓心。
- F_1 是接觸雪面 P 施與滑雪者的支撐力,在 x 軸的分量。
- N_1 是接觸雪面 P 施與滑雪者的支撐力,在 y 軸的分量。
這裡滑雪者 G 的瞬時速度 v 是指出紙面(螢幕)的。
在質心 G 在總力平衡的條件下,y 軸方向的總力(加速度)為零。也就是說,當滑雪者轉彎的時候,y 方向的總力為零可以表示為:
N_1 – m g cos(alpha) = 0 (1)
這裡 m 是滑雪者與雪板的質量總和。考慮牛頓第二運動定律,在 x 軸上:
F_1 = m g sin(alpha) cos(beta) = m a_c (2)
而向心加速度可以表示成:
a_c = v^2 / R_T
將之代換到 (2) 之中,我們可以將整個系統近似成一個轉動慣量平衡,也就是對於質心 G 而言總角動量為零。可以用以下數學式表示:
F_1 sin(theta) L – N_1 cos(theta) L = 0 (3)
結合 (1) – (3) 式,我們可以得到:
tan(theta) = g cos(alpha) / g sin(alpha) cos(beta) + v^2/R_T
請注意這裡質量 m 與長度 L 已經不需要了,因為他們已經在式子中約掉了。
這個式子要怎麼用呢?舉個簡單的例子:
當某個瞬間 alpha = 20 度(這要算紅道還是藍道?),beta = 60 度,速度 5 m/s (時速 18 公里),雪板側邊的弧度半徑 14.8 公尺,雪板與雪面交角 phi = 30 度。這樣子傾角 theta 應該是多少呢?
要達到完全割雪轉彎 R_T = R_SC,所以 R_T = R_SC cos(phi) = 14.8 cos(30) = 12.82 m,也就是 theta = 68.5°
當在坡面上滑雪的時候,在轉彎的過程中迴轉半徑 R_T 不會是一個定值,會有變動是正常的。尤其是重力的分量對於滑雪者在轉彎的軌跡中,如同 (2) 所示,beta 會隨之改變。自然地,滑雪者的傾角,還有雪板與雪面的交角 phi 也要配合調整,最後達到改變 R_T 的目的。這使得滑雪的物理分析變得複雜。
下一個部份,我們要來分析這個雪板切入雪面的角度,來避免在雪上發生側滑。
在此之前,有一些預備知識需要先來了解。
避免雪板在雪面上側滑
這裡有兩個雪板物理學考慮的點:滑雪板如何會發生側滑,還有如何來避免。
首先,當雪板在一個水平而且平坦的雪面上時,只要滑雪者腳對雪板的施力,
與雪板的平面成90度,就可以避免發生側滑。這是由於雪面與雪板間的摩擦力非常小,只要有一點點橫向的分力,就會使得雪板(側向)滑動。
第二點是當雪板在斜坡雪面上時,滑雪者必須以一個傾角將雪板壓入雪中,才能防止滑動。如此一來,滑雪者施在雪板上與雪板面平行的分量,成為是指向雪中的力量。
我們以下面的圖示來說明: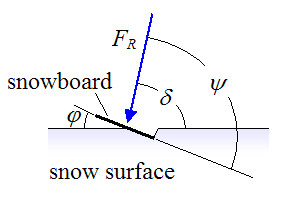
滑雪者施力於雪板,避免在斜坡上發生滑動,其中:
- phi 是滑雪板與雪面的傾角
- delta 是施力方向與雪面的交角
- psi 是施力方向與滑雪板面的交角
- F_R 則是滑雪者的腳施與滑雪板的合力
要避免滑動, psi 角必須大於或等於90度。這也就是說 F_R 力平行於滑雪板面的分量,必須為零(當 phi = 90度),或是指向雪中(往山峰或迴轉中心),也就是往右(當 phi > 90 度),如此一來雪面就像是一面高牆,擋住雪板滑動。
然而當 psi 角小於 90 度時,F_R 在平行於滑雪板面的分量,會往迴轉外側(往山谷),也就是往示意圖的左方。(將雪板帶離雪板壓出的溝)請注意我們這裡忽略了雪板本身的重量,所以實際上的關鍵角度將不同於90度。
就地形而言,要避免側向滑動,delta 角必須大於或等於 90 – phi。
我們可以用上一節的簡單例子,來驗證前述的物理。
首先必須檢查(滑雪者的腳)施力 F_R 與滑雪板的角度。這裡忽略相對較小的滑雪板質量,這力等於 F1 與 N1 施予滑雪板的大小,但方向相反。由於系統是旋轉平衡(沒有旋轉/力矩),也就是說 F1 與 N1 都會通過質心 G 點。即 delta 角相同於前面的 theta 傾角。當 delta = 68.5度,是大於 90 – phi = 60 度的。因此滑雪板不會發生側滑。
空中特技
滑雪者可以在空中表演的一些特技、旋轉、翻滾等,基本上是藉由角動量的守衡來達成的。當滑雪者離開地面後,總角動量就不能再改變了。因此在離開地面前,需要給自己一個初始的旋轉,然後藉由身體姿勢的改變,來達成這些驚人的動作,並保持總角動量守衡。
對這些空中特技來說,滑雪板背後的物理跟滑長板是非常類似的。(所以雪季過後,就要靠長板來止癢了!)
照片顯示滑雪者前轉180度
下一節將介紹半管中如何加速。
在半管中加速
下面照片顯示滑雪者脫離半管進入空中。
滑雪者可以在半管中加速,維持雙腳固定在雪板上,這是如何達成的呢?這個現象背後的基本物理,是可以由轉動慣量與角動量來理解的。
為了增加速度,滑雪者在直線段蹲低,當進入半管的曲面時,站起身來並舉起雙手,讓自己可以在離開半管時有更高的速度。
以下說明滑雪板物理在半管的機制: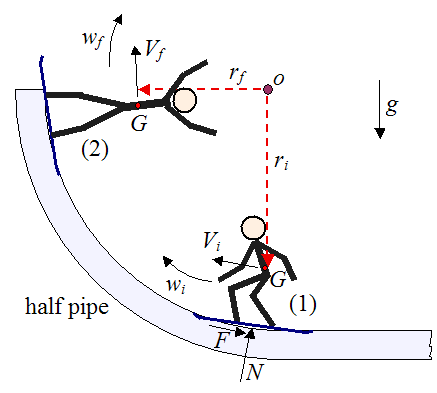
這裡
- w_i 是初始滑雪者身體的角速度,於位置 (1)
- w_f 是最終角速度,於位置 (2) 也就是脫離半管的位置
- V_i 是初始質心 G 速度,於位置 (1)
- V_f 是最終質心 G 速度,於位置 (2)
- r_i 是初始迴轉半圓圓心 O 與質心 G 的距離,於位置 (1)
- r_f 是最終迴轉半圓與質心 G 的距離,於位置 (2)
- g 是重力加速度
- N 是地面施與雪板的作用力
- F 是地面施與雪板的摩擦力
這裡假設半管是理想的半圓,圓心在 O,並且簡化成二維空間分析。在總角動量守衡下,我們來看轉動慣量與角動量的方程式:
I_oi w_i + Sum Int{t_i, t_f} M_o dt = I_of w_f
I_oi 是初始轉動慣量(滑雪者加雪板),於位置 (1)
I_of 是最終的轉動慣量,於位置 (2)
Sum M_o 是對於 O 這點的動量的總和,動量由開始時間於位置 (1) 積分到最終的時間於位置 (2)。
這裡我們假設以剛體處理,即使滑雪者的轉動慣量在這兩點之間有改變。就結論而言,我們只需要知道起始點與終點身體的轉動慣量大小。
由於地面對於滑雪者的作用力 N 通過 O 點,所以不會造成角動量的變化。摩擦力 F 夠小,在這裡可以忽略不記。所以剩下來的,就只有重力 g 對於滑雪者與 O 點的貢獻。(這裡同時考慮滑雪者與雪板)
我們可以將 w_f 獨立出來:
w_f = (I_oi w_i + Sum Int{t_i, t_f} M_o dt) / I_of
I_oi = I_Gi + m r_i^2
I_of = I_Gf + m r_f^2
這裡,對於位置 (1) 和 (2) 的轉動慣量為:
I_Gi 是初始轉動慣量在 G 上於位置 (1),向垂直頁面往外的方向。
I_Gf 是最終轉動慣量在 G 上於位置 (2),向垂直頁面往外的方向。
m 是滑雪者的質量
在以上的方程式中,我們減少 I_of,而角速度 w_f 可以比原先(不改變 I_of)增加的更多。實務上,我們可以藉由減少質量中心 G 到 O 點的距離來達成。換句話說,減少 r_f 可以增加 w_f。要注意一點,實際上 I_Gf 跟 Sum M_o 也會改變,但主要的貢獻在於 r_f。
在位置 (1) 和 (2),質心 G 的速度可以表示為:
V_i = w_i * r_i
V_f = w_f * r_f
滑雪者的質心速度在位置 (1) 和 (2)
這兩個速度在位置 (1) 和 (2) 都與半管的曲面平行,這裡我們假設剛體運動。
以上關於速度的方程式,假使滑雪者能將 r_f 減到夠小(藉由起身並舉起雙臂),將可以有效地增加角速度 w_f。這將可以讓脫離半管時的速度 V_f 達到更高。
藉由連續地在曲面上的往復運動(在半管最低點蹲低然後起身並舉其雙臂),滑雪者可以持續地增加速度,最後可以達到足夠的高度來從事不同的空中特技。
用一個更直覺(不用數學)的說法來解釋,藉由往復運動(pumping)來對系統所做的功,可以轉變成離開半管時更快的速度。我們可以將此類比於小朋友盪鞦韆時,以蹲起的動作,來增加擺盪加速而盪得更高的方式一樣。當然這背後的物理也是類似的。
在滑雪者起身並舉起雙臂的過程中,他將會感受到由於旋轉造成的向心力,將他由 O 點往外的方向推開。這阻力證明了滑雪者所做的功,會轉成能量加到系統當中,最後形成更高的動能(速度)與位能(高度)。
最後一小節,我們來看關於滑雪板的保養,來維持最佳表現。
滑雪板保養
滑雪板的保養,基於滑雪板的物理,在於最佳化雪板在雪面上的表現,可以歸納為以下幾點:
- 將雪板與雪面接觸的表面上蠟,可以防止水侵入造成雪板的損壞。蠟也可以避免雪板底部有過多的水蓄積,來減少潮溼表面的阻力(吸附力)。
- 將雪板的板邊用磨石磨利,將有助於轉彎與板邊的控制。